목적
- Deep learning의 경우에는 일반적으로 결과에 대한 해석이 black-box 인 것으로 알려져 있음
- 최근에 이미지 데이터의 경우에는 gradient 기반으로 class 산출 결과에 대한 해석 방안이 언급되고 있음(Ex. grad-CAM 등)
- gradient 값을 활용하여 class 예측에 주요 영향을 주는 input variable을 찾고자 함
가정 사항 및 접근 방법
- deep learning 학습 시 weight matrix 의 경우에는 input data에서 주요 의미가 있는 feature에 대해 추상화 작업을 하는 것으로 의미적으로 해석이 가능함
- 학습된 deep learning 모형을 대상으로 하여 feature 특성을 발현할 수 있는 loss를 강제로 생성함
- 해당 loss에 대해 back propagation을 수행하여 최초의 weight matrix의 gradient 값을 계산함
- 해당 gradient에 대해 input feature 단위로 summary를 한다고 하면 해당 feature별로 발현되는 gradient 값을 산출 할 수 있음
- 이 때 gradient 값이 큰 feature가 해당 class를 설명해주는 주요한 feature일 것이다.
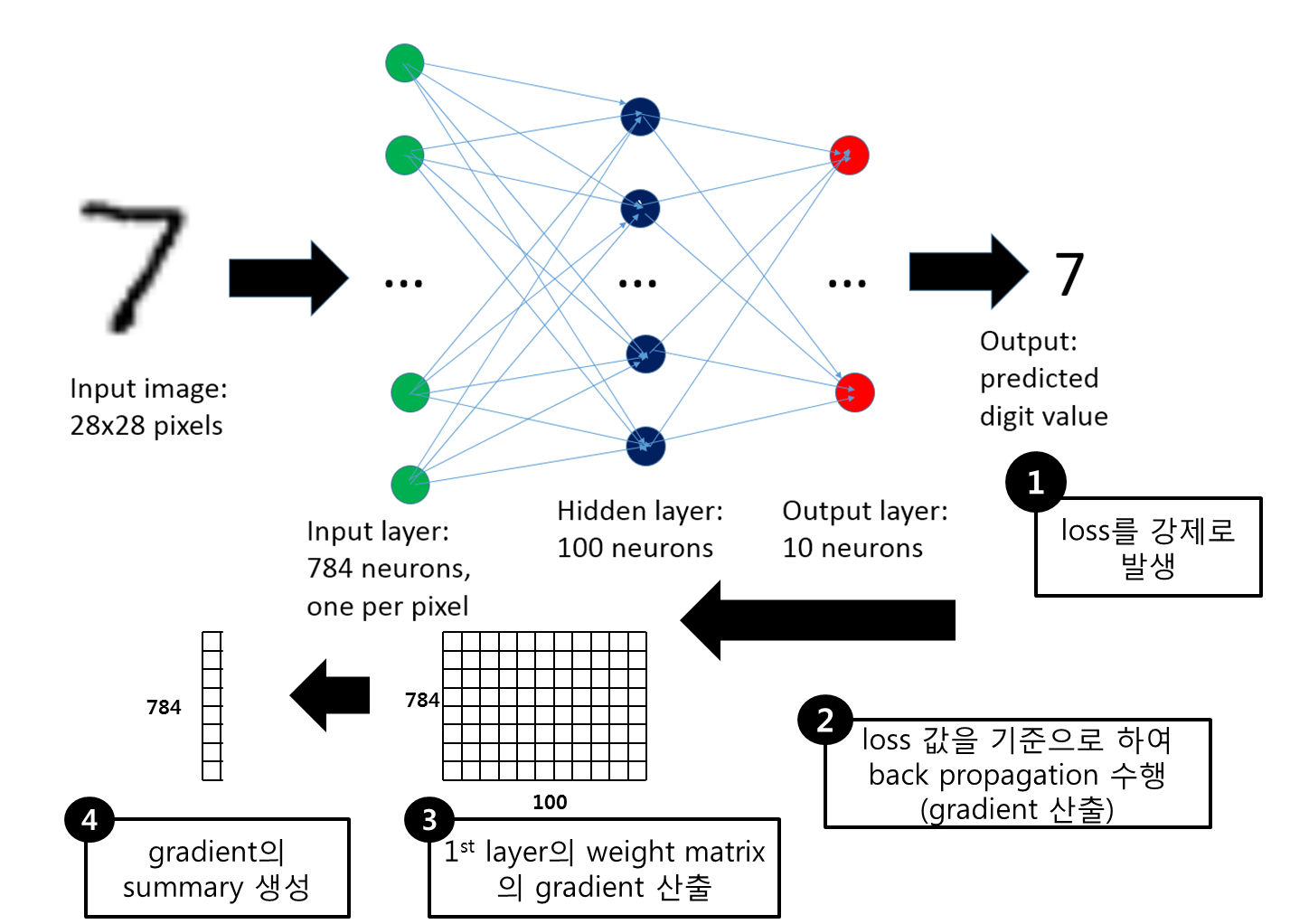
Test 수행 Approach
- 결국은 loss를 어떻게 생성하는지가 해당 방법에서 가장 중요한 사항임
- loss 생성 관련 해서 다양한 테스트를 수행하여서 적합한 방법을 찾아보고자 함
Network 생성
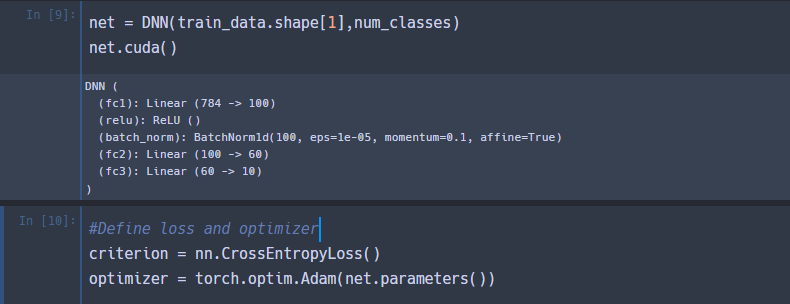
- 3개 layer로 구성된 DNN 생성
- 각각 layer에 activation 함수로 ReLU 적용
- 최종으로 softmax 를 적용하여 각 class 별로 확률을 생성 하였으며, loss는 CrossEntropy를 적용함
- loss는 Adam 적용(lr = default)
- train 데이터 기준 20 epoch수행
Concept Test
Approach 1
- input 데이터를 기준으로 하여 전혀 다른 label 값을 부여하여서 loss를 발생시킴
- 해당 class로 데이터를 fitting 하기 위해 1st layer에서 gradient 수정이 발생함
- gradient 값의 변화가 생기는 부분이 바로 원래 input data의 특성을 나타내는 부분 일 것이라는 가정으로 출발함
- Test 수행 process
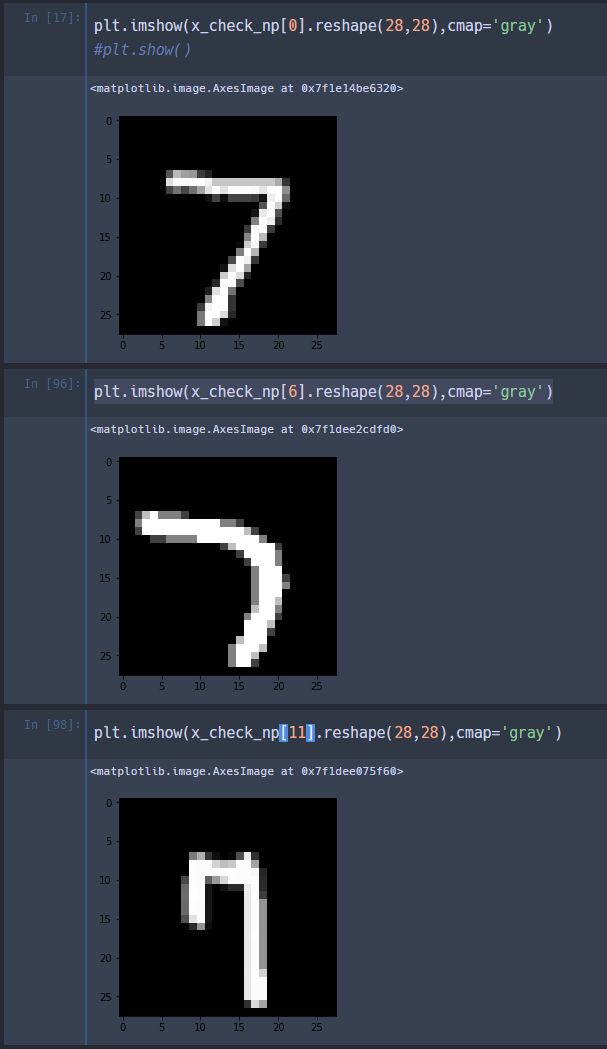
- MNIST 데이터 중 7번 class의 데이터를 100개 추출 - 해당 데이터에 대한 label을 0으로 강제 할당함(강제로 다른 label을 할당함) - loss를 산출하고 1st layer 의 weight의 gradient 값을 산출
- dimension을 input data와 동일한 형태로 변환
- sum, mean 두 가지 방법을 사용해 보았으니 큰 차이점은 없음
- 해당 Test에서는 mean 방법을 적용
- 해당 결과에 ReLU를 적용
- Test 수행 결과
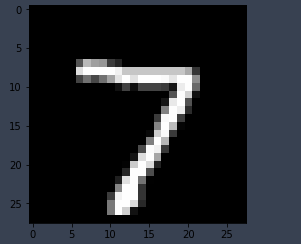
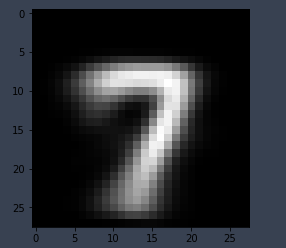
| Input Data | gradient Data |
|---|---|
 |
 |
-
input data의 특징알 가지는 형태로 gradient 값이 산출됨
-
여기서 의미있는 점은 input data의 경우에는 다양한 형태를 가지고 있으나 gradient 산출 결과는 이를 반영한 일종의 표준 형태라는 점임
Approach 2
- Test 수행 process
- Approach 1과 기본적으로 동일한 방법으로 수행하나 label을 해당 label을 그대로 사용
- 1st layer의 weight의 gradient 산출
- 해당 gradient 값에 대해 1/(1-gradient) 형태로 값을 변환
- Test 수행 결과
| Input Data | gradient Data |
|---|---|
 |
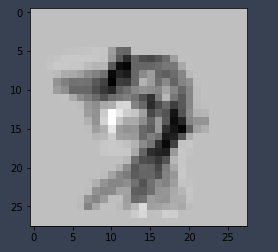 |
- Approach 1 보다 결과가 좋지 않음
- 1-gradient 값을 활용하였기 때문에 음영이 바뀌어서 나옴
- 해당 클래스 만의 특징을 추출 하였다고 보기 어려움
Approach 3
- loss 를 기존과 다른 방법으로 산출함
- 1,2 의 경우에는 각 class별 확률 값을 기준으로 하여 loss 산출 결과를 활용함
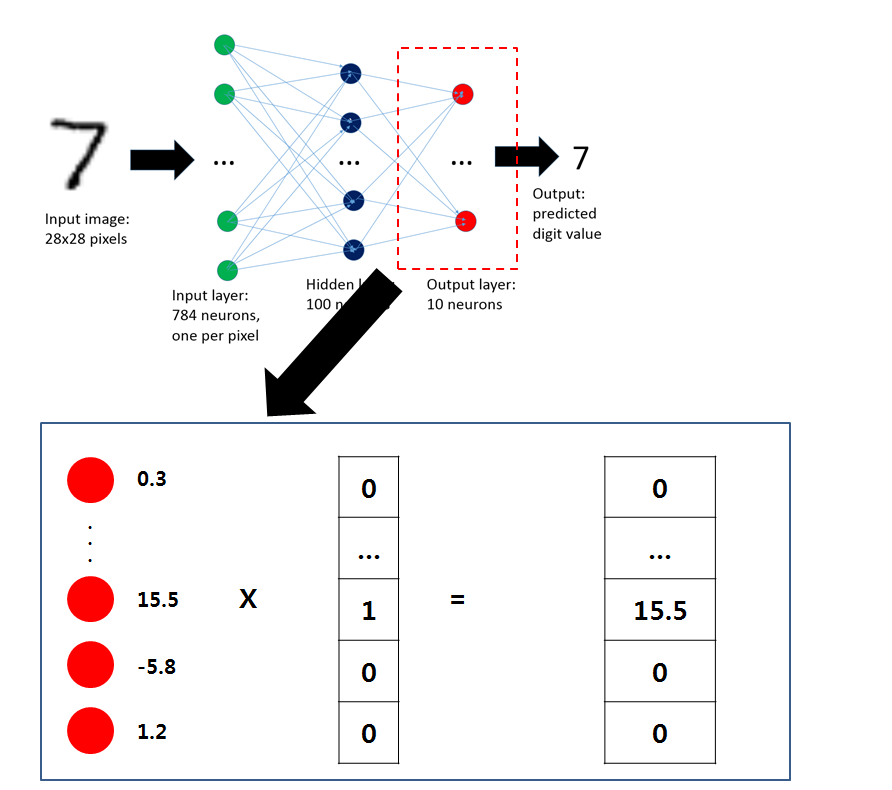
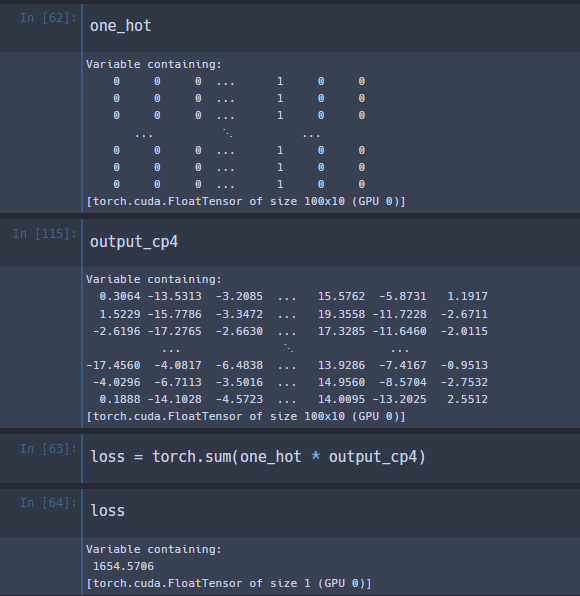
- softmax를 통과하기 이전의 값을 기준으로 하여 해당 class의 값 만을 합한 형태로 하여 loss를 산출함
-
이후 방법은 Approach 1,2의 방법과 동일함
-
Test 수행 결과
| Input Data | gradient Data |
|---|---|
 |
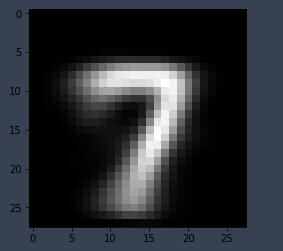 |
- Approach 1 과 유사한 결과를 보임 - Approach 1의 경우에는 다른 Class를 어떤 값으로 설정하는지가 gradient 산출에 중요한 영향을 주나 Approach 3의 경우에는 해당 Class만의 특징을 산출하는데에는 더 적합할 것으로 보임
Approach 4
- Approach 3 + Approach 1의 방법으로 활용
- 전체적인 방법은 Approach 3의 방법을 활용하나 정답지 라벨을 기존 label과 다른 값을 선정함
- gradient 값이 음수로 나오기 때문에 산출한 gradient 값에 -1 을 곱함
- Test 수행 결과
| Input Data | gradient Data |
|---|---|
 |
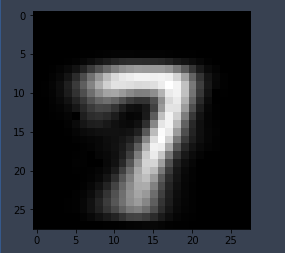 |
결론
- first layer의 weight matrix에서의 gradient 값을 활용하여 input data 에서 의미있는 feature를 산출할 수 있을 것으로 보임
- 4가지 방법을 적용하여 test를 수행하였는데 3,4 번의 방법이 활용 관점에서 적절할 것으로 보임
- Approach 3의 경우에는 해당 Class의 특징을 산출하는데 활용할 수 있음
- Approach 4의 경우에는 다른 Class와 비교하여 어떤 차이점을 알고자 할 때 활용할 수 있음